辯與辨: 走出 「畫等號」 的辯論思維
By HUNG Chao-Kuei on Sunday, February 15 2009, 18:42 - Permalink
- 隨時自省自己是否掉入這個圈套當中;
- 用這篇文章提醒對手 (還有支持自己論點的盟友) 就事論事, 不要轉移話題/模糊焦點/貼標籤;
- 有一個公式, 可以破解對手採用這種策略。
同時也希望旁觀, 未發言的沈默大眾, 更可以明辨辯論者的論點高下, 而不被 「畫等號辯論法」 誤導離題。 也希望更多 3*3 的九宮格取代 1+1 的對立圖, 讓臺灣人可以更加頭腦清楚地就事論事, 讓二元對立的文化走向多元包容的文化。
* * * * *
| 「P」 主張 | p1:追查密帳 | p2:採用開放格式 | p3:爭取言論自由 |
|---|---|---|---|
| 「Q」 類別 | q1:禿頭 | q2:學術無成 | q3: 被利用的年輕人 |
| q1': 支持X民黨 | q2': 支持開放原始碼 | q3': 支持民X黨 | |
| q1'': 支持統一 | q2'': 反微軟 | q3'': 支持正名 |
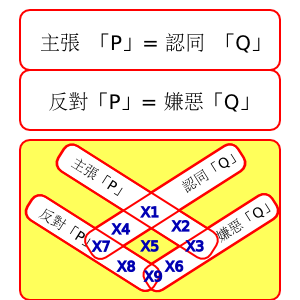
某甲主張 P。 P 可能是 「追查密帳」, 可能是 「採用開放格式」, 可能是 「爭取言論自由」 ... 。 但是可能因為某甲的人緣不好, 態度過激, 地位不高, ... 等等因素, 總之有一群人跳出來抨擊某甲。 他們把某甲歸類為 「認同 Q 類別的人」。 於是正方或反方, 可能有意或無意地, 把這個議題變成如圖的上半; 而旁觀的沈默大眾也被迫在心中回答一個 [錯誤的] 問題: 「我到底屬於這兩塊當中的那一塊?」 然後本來討論議題 P 正反兩面的人, 開始討伐 Q 類別的人或是替他們叫屈。 最後大家就忘記 P 議題的重要性。
在這樣的爭論之中, 經常還是可以看到一個細小的理性聲音, 但是這個聲音常常被埋沒: 「主張議題 P」 真的就等於 「認同類別 Q」 嗎? 其實道理也很簡單: 既然是兩句話, 當然可以分開討論。 就議題 P 而言, 可能有 「支持者」, 「反對者」, 及 「不表意見」 三類旁觀大眾。 就對於類別 Q 的態度而言, 也可能有 「認同者」, 「嫌惡者」, 及 「不表意見」 三類旁觀大眾。 所以事實的全貌, 應該有 3*3 種組合, 如圖的下半。 當然, 這九塊的大小, 可能相去甚遠, 完全不成比例, 而不是圖中畫的那麼整齊。 針對每個議題, 去調查這九塊的比例, 應該是很有趣的社會研究題目。 但無論如何, 重點是: 事實有九塊, 而不是兩塊。
如果類別 Q 是無關議題 P 的單純人身攻擊 (高矮胖瘦/婚姻狀況/生活習慣/...), 這很容易對付。 某甲只需要說: 「我是不是 Q, 跟要不要主張 P, 有什麼關係? 是 Q, 或不是 Q, 就沒有權利主張 P 嗎?」 大多數臺灣人的判斷力, 已經超越這個層次。
如果類別 Q 是一種能力, 社會地位, 或是一種道德操守 (判斷力/健康/學術成就/外遇記錄/...), 且與議題 P 相關, 那麼某甲還是可以處理: 「我可能是 Q, 也可能不是 Q; 但我有那麼重要嗎? 我是不是 Q, 會影響 P 這個主張的正當性嗎? 討論我是不是 Q, 就不必回答 P 是否正當的問題了嗎? 請就事論事, 請別離題。」 當然, 本文不適用於一類狀況: 如果議題 P 的文字直接提及某甲, 例如是 「選XX當YY」, 這類關於選舉的議題, 那麼把 P 與 Q 連在一起談, 有時候也可能有一些正當性。 這類議題, 並不是本文要處理的。
最難處理, 也是促成我寫本文的常見狀況, 是: 類別 Q 是一個顯眼的族群, 例如某宗教/某政黨/..., 而且在直觀上, 確實經常與議題 P 有相關性。 也就是說, 在此狀況當中, 議題 P 的支持者 (反對者), 與認同 (嫌惡) 類別 Q 的人口, 有高度的重疊性; 或者用圖來說, 就是圖中的 X1 與 X9 兩塊特別大, 可能是最大兩塊, 也可能是第二大第三大兩塊 -- 僅次於完全沒意見的 X5。 於是他們的聲音通常最大。 他們在 P 議題上對立; 他們在面對 Q 類別人口的態度上, 也對立。 X1 裡面有一部分 「P=Q 畫等號族」, 不斷地把 X7 和 X8, 硬貼上 「嫌惡 Q」 的標籤, 說他們根本是 X9 偽裝的; 對稱地, X9 裡面有一部分 「P=Q 畫等號族」 則不斷地把 X2 和 X3, 硬貼上 「認同 Q」 的標籤, 說他們根本是 X1 偽裝的。 在這些 「P=Q 畫等號族」 的眼裡, 看不見其他七塊 (頂多承認 X5)。 X1 與 X9 處處對立; 但是 X1 裡面的 「畫等號族」 與 X9 裡面 「畫等號族」 在 「強化二元對立」 這件事情上, 卻是合作無間, 共同曲解九宮格其他位置的人的態度與立場。 然後下一個議題 p2, 他們還是找同一個類別 Q 來畫等號。 或者把先前 p1 議題當中的 「Q 的相反」 拿來當 p2 議題當中的 Q, 角色對調一下, 但 「畫等號」 的動作還是一樣。 然後對很多不同的議題 p3, p4, ... 都找 同一組 Q 和 Q 的相反來畫等號。 學過一點近代代數, 知道 equivalence class 與 transitive closure 的人, 再加上一點數學歸納法, 都知道接下來會發生什麼事; 沒學過的人, 用直覺想, 也知道: 經過很多議題以後, 臺灣就只剩下兩類人: Q 和 Q 的相反。 這, 就是二元對立的病源。
上面這一段, 真的值得您深思。 請讓它沈澱一下。
變成抽象的文字, 道理很簡單, 扣除掉書袋的部分, 也許連邏輯清楚的高中生都聽得懂 (我甚至是用剪貼修改的方式寫出上面對稱的兩句話) 但是把抽象的 P 與 Q 代換成具體的熱門政治時事或政黨名稱時, 您我就失去理性了。 真的, 我自己也犯過相同的錯誤。 臺灣二元對立的病源, 不是因為有很多不同的意見, 而是因為我們有 「畫等號的辯論態度」。 歐美許多國家的人民也有很多分歧的意見, 但他們不見得有二元對立。 我不相信華人具有奴性 (oh no, 別再畫等號了), 我不相信西方人就可以有尊重不同意見的多元文化, 而華人的民族性就是必須忍受獨裁壟斷, 二元對立, 或者一團亂。 我相信: 停止盲目地畫等號, 讓九宮格的其他七塊出現, 小而觀之, 可以更理性地討論每一個 P; 大而觀之, 可以讓臺灣從二元對立走向多元包容。 因為大家終於會相信: 對於不同的議題 p1,p2,p3,... 認同 Q 的人可以有不同的態度, 有些時候甚至會與 嫌惡 Q 的人並肩或對調位置。 用發言者所屬的 Q 類別來決定 p1,p2,p3,... 的正確性, 不如就每一個 P 的優缺點直接討論。 我們終於可以逐漸學會 「不以言廢人」 「不盲目崇拜聖賢」 的理性辯論態度。 (何況這些大聲講話的人, 都還不是廢人, 也不是聖賢, 我們更沒道理那麼在乎一定要與他站在同一陣線或相反陣線。)
以上爭取您的認同。 以下是具體的策略建議。
首先給一個簡單的公式: 建議位於 X1 的朋友們, 請積極地在 X3 當中尋找盟友。 這是拆解 「畫等號的辯論」 的最佳策略。 而且, 一旦獲得 X3 發聲支持, X2 當然也就更敢發聲支持 P。
位於 X1 的議題 P 支持者, 要叫他去找出而且肯定 X3, 可能會有很大的心理障礙, 因為 X3 嫌惡類別 Q。 但是請想清楚: 對您而言, 到底是議題 P 比較重要, 還是類別 Q 比較重要? 到底您現在是在說服眾人支持議題 P, 還是在尋找 Q 黨同志的溫暖? Q 黨同志會因為您肯定 X3 而與您反目嗎? 而且, 如果您不願意友善對待 X3 的朋友, 但對手 X9 卻願意友善對待 X7 的朋友, 那麼很可能吃虧的不只是議題 P, 甚至連您認同的類別 Q 也會吃虧。
因為還有沈默的 X5 在觀察。
沈默的 X5 可能不會公開表達意見; 但是在投票, 推薦/轉寄/書籤/Twitter文章, ... 的時候, 很可能具有相當影響力。 這些人的人口, 可能遠遠超過大聲講話的 X1 與 X9; 但是因為他們不發聲, 以致於他們的重要性經常被遺忘。 X1 以為自己在跟 X9 爭論; 但其實是這兩群人在表演給其他七群人看。 當這七群人 (尤其是 X5) 看到 X9 包容 X7, 而 X1 打壓 X3 的時候, 您說他們會傾向支持誰?
特別奉勸 X1 自己, 千萬別施展 「P=Q 畫等號的辯論」, 別用這種方式對抗 X9。 如果您也屬於 X1, 而看到 X1 的盟友這麼做, 請跳出來拿這篇文章勸阻他; 如果您屬於 X9, 看到 X1 施展 「P=Q 畫等號的辯論」, 也請拿這篇文章出來, 但主要是要給 X4 與 X7 看。 為什麼?
先從 「對 Q 的態度」 這個角度分類, 來看一下圖中的 "中間選民"。 中立, 或中間選民的意思, 並不是永遠不表達意見。 矇上眼睛, 不去看議題 P 的爭議, 塞住耳朵, 假裝爭議不存在, 這都不叫 「對 Q 中立」。 選擇一個曖昧的立場, 把 P 和反 P 都罵一遍, 這也不代表 「對 Q 中立」。 對 Q 中立, 還是大可以在不同的議題 p1, p2, p3, ... 當中, 理性地選擇與多數的 Q 站在同一側 (X2), 相反側 (X8), 或者就這個議題不發表意見 (X5)。 再強調一次: P 與 Q 是分開的兩件事; 對類別 Q 態度的中間, 並不表示對 P 就一定不能有意見。 以 「對 Q 的態度」 來分類, X2, X5 與 X8 都是所謂的 「中間選民」。
X1 如果開始採用 「P=Q 畫等號」 策略, 把 X7 與 X8 硬是歸類為 X9, 那麼會有幾個效果: (1) X8 不敢聲稱他反對 P (2) 未來如果有機會, X8 將傾向行動支持 「Q 的相反」。 (3) X7 會感到很困惑惶恐。
我對於 X4 與 X7 的態度特別有興趣。 這次, 您並不特別支持議題 P, 甚至反對議題 P, 但基本上您認同類別 Q; 如果您發現: 在討論 P 的場合, 經過勸說之後, X1 仍然拒絕包容 X3, 而且硬要把 X7 與 X8 歸類為 X9, 您應該怎麼做? 如果是一次兩次, 就算了; 如果這樣的狀況一再發生, 而您發現自己經常從不在乎的 X4, 甚至從不敢說出口的 X7, 莫名奇妙地變成 X1, 但並不是因為每個 P 都很有道理, 只是因為如果您與 X1 距離太遠, 會有被 X1 誤解的危險, 那麼您應該認真思考一下: 「當初為什麼我會認同類別 Q? 是因為追隨大人物, 還是因為認同事理?」 竊以為: X4 與 X7 人口的覺醒, 是臺灣社會整體進步的重要關鍵。 特別是 X7, 社會能否允許他們大聲說話, 將決定臺灣能否走出二元對立。
以上的一切, 反過來也成立: 反對議題 P 的朋友們, 應該積極地在 X7 當中尋找盟友。 因為如果對手 X1 包容 X3, 而 X9 卻傻傻地打壓 X7, 那麼 X5 很可能傾向遠離 X9, 傾向支持 P, 因為他選擇支持議題 P 的時候, 還可以保有選擇認同 Q 或嫌惡 Q 的自由。 如果 X9 開始採用 「P=Q 畫等號」 策略, 把 X2 與 X3 硬是歸類為 X1, 那麼 X2 會噤聲, 看起來好像您贏了, 但將來他可能更加默默地支持類別 Q。 X9 如果施展「P=Q畫等號」策略, 還會讓 X3 與 X6 感到困惑惶恐。 一次或兩次, 短期內, 畫等號策略可以把 X3 與 X6 拉來反對這次的議題 P; 但長期下來, 如果夠多 X3 與 X6 覺醒, 認清楚 「支持畫等號策略會造成社會二元化」, 那麼這個策略反而可能會傷害到 「Q 的相反」, 也就是 X9 所認同的類別。 社會能否允許 X3 大聲說話, 將決定臺灣能否走出二元對立。
所以, 懇請邏輯清晰的辯論者做兩件事。 第一, 請把您的議題, 代入上面的符號, 得到的白話文, 轉述給您的討論版聽。 希望這對您的討論有幫助。 第二, 如果您想出或看到一些類似上文, 適用於任何 P 與 Q 的通用論點, 可以勸阻 X1 與 X9 施展 「畫等號的辯論」, 或是可以鼓勵位於其他七格的朋友看破 「畫等號的辯論」 的手腳. 也請將您手邊那一段 [僅適用於您所談論議題情境的] 白話文裡面的具體名詞拿掉, 改成 "P" 與 "Q", 貼在這裡, 分享給其他辯論者參考。
又, 可以想見, 用具體的名詞取代 P 與 Q 之後, 還是會有人跳出來, 指稱我寫這篇文章, 根本就是因為我同情或厭惡某個類別, 才硬拗出來的; 篇文章又會被某些 X1 或 X9, 拿來與某個類別 Q 畫上等號 :-) 這篇文章這麼長, 又像是數學邏輯的證明論文, 誰那麼用心看? 能說服多少 X3, X4, X6, X7 呢? (不必理會堅持畫等號的 X1 與 X9, 因為他們的堅持, 是他們的損失。) 這裡有一個很簡單的邏輯: 這篇文章沒有辦法預設立場; 這篇文章從兩面看, 是對稱的。 (但並不是四面對稱) 您的議題可以代成 「支持 P」, 也可以稍微改寫, 改成 「反對 P」, 其餘對稱修改。 (Xi 改成 Xj, i+j=10) 這篇文章, 是一個預先寫好, 公開原始碼的程式。 這篇文章, 沒辦法見招拆招, 遇到什麼議題, 才刻意去找一個立場。 這篇文章如果有錯, 是錯在邏輯 (歡迎指正), 而不是錯在立場。 懷疑者只需要自己驗證翻譯過程是否忠實, 而不需要讀完抽象的全文, 就可以確認: 這篇文章, 沒有立場。 這篇文章的目的不是支持 P, 也不是反對 P。 這篇文章最重要的目的, 是告訴九格內的所有人: 製造二元對立的, 既不是 P 的支持者, 也不是 P 的反對者; 既不是認同 Q 的人, 也不是嫌惡 Q 的人。 製造二元對立的, 是不合邏輯的 「畫等號」 的習性。 請大家在討論每一個議題 P 的場合, 先是重覆輕聲提醒幾次, 然後是嚴正譴責堅持畫等號的人。 請大家共同讓 「畫等號」 變成一個不受歡迎的辯論方式。
我自己呢, 也要回到我熟悉的軟體場域, 開始拆解自己過去無知覺/無意識時, 不小心所畫出來的等號; 也請大家幫忙, 如果發現我在任何文章留下 「畫等號」 的言論, 請在那一篇留言指正。 希望臺灣人可以就事理爭辯, 可以明辨辯論者論點的高下, 而不是就類別 (政黨/統獨/...) 分別是否同我族類。 希望臺灣人可以走出 「畫等號」 的辯論思維, 擺脫二元對立的掙扎, 走向理性包容, 允許不同意見排列組合的多元文化。
![[rss feed 圖案]](/~ckhung/i/rss.png)
Comments
「…對 Q 中立, 還是大可以在不同的議題 p1, p2, p3, ... 當中, 理性地選擇與 Q 站在同一側 (X2), 相反側 (X8), 或者就這個議題不發表意見 (X5)。…」
後一個Q是不是打錯了?應該是P吧?
哇, 這篇竟然真的還有朋友認真看 :-)
兩個都是 Q 沒錯。 因為多數的 Q 都支持 P, 所以 「主張議題 P」 的人, 經常被歸類為 「認同類別 Q」; 但事實上對於議題 P1, 他可能與類別 Q 的主張相同; 對於議題 P2, 他可能與類別 Q 的主張相反; 對於議題 P3, 他可能沒有意見。 如果只因為他在 P1 這個議題上正好與多數的 Q 相同, 就把他歸為類別 Q, 就否定他對於類別 Q 的中立性, 那麼這樣的批判就掉入二元思維了。 這正是本篇企圖解釋的重點。
謝謝雪凡幫忙 debug; 現在把第二個 「Q」 改成 「多數的 Q」, 讓文意更明顯。
喔,原來如此,我把第二個 Q 當作「立場」,但格主的意思是「持有 Q 立場的多數人」對吧。
其實看前後的文意還是可以推論出來的,邏輯思辨能力還是不夠強啊>_<
這次偶然經過貴寶地,意外發現很多奇思妙想的碎片,看樣子以後不得不常常來拜訪了。
This post's comments feed