愚公移山與遞迴
愚公移山法
有一些問題, 乍看之下很困難; 再仔細想想其實只是很耗時, 流程未必很複雜。 如果暫不考慮效率 (反正辛苦的是電腦, 又不是人) 不考慮程式的優雅美觀, 只是單純地將所有可能的答案逐一產生出來, 其實程式並不難寫。 以這種想法寫出來的這類演算法/程式, 通稱為 brute-force algorithms。 有人譯為 「暴力演算法」; 筆者偏好稱之為 「愚公移山法」。
舉幾個例子:
- 給你 1 個正整數 s 與另外 n 個正整數 x(1), x(2), ..., x(n), 請從這 n 個正整數當中挑選一些出來, 讓它們的總和為 s。 這個問題叫做 subset sum。
- 在 5x5 縮小版的西洋棋盤上, 一個騎士 (類似象棋的馬) 從角落出發, 希望以 24 步走完棋盤, 也就是必須每格恰好踏一次, 沒有重複也沒有遺漏, 請找出一條可能的路徑。 perl 版; c 版 (這其實是一個 Hamiltonian Path 問題。)
- 西洋棋的皇后可以攻擊同列, 同行, 及對角線上的其他棋子。 在 8x8 的盤上, 如何安置最多個皇后, 讓她們彼此相安無事? (這其實是一個 Maximum Independent Set 問題。)
如果你希望 「很快, 很有效率地 找出答案」, 那麼這些問題都很困難 -- 事實上, 上面列舉的問題剛好都屬於 NP problems, 世界上沒有人知道如何用一般的電腦, 在 polynomial time 時間內解決。 另一方面, 如果我們不要求效率, 可以接受花費 exponential time 的時間, 那麼很容易就可以得到一個 exhaustive search 演算法 -- 不厭其煩地產生所有可能狀況, 並逐一測試是否符合題目條件, 是否比先前找到的答案更好, 直到所有可能狀況測試完畢。 至於如何 "產生所有可能狀況" ? 通常都可以 (也需要) 用遞迴 -- 程式設計師會說這是 "一個副程式, 自己呼叫自己 (而它還會呼叫自己...)"; 孫悟空會說這是 "拔幾根頭髮, 叫出幾個小孫悟空來幫忙 (而他們還會拔他們自己的頭髮...)"; 老鼠會成員會說這是 "請別人幫自己賺錢 (而他們還會請其他人幫忙賺錢...)"。
撰寫遞迴程式有幾個最重要的原則如下 (細節後面詳述):
- 將原問題拆成幾個 長相類似原問題 的新問題
- 每個新問題必須比原問題都 更小 (即使只小一號也可以)
- 面對夠小的問題時, 就 直接解決, 不可以無限遞迴下去
電腦如何處理遞迴程式?
所謂 遞迴 (recursion), 就是一個副程式執行到半途, 還沒有完全結束時, 又呼叫自己。 下面的例子使用遞迴的方式, 來計算階乘 (6! = 6*5*4*3*2*1):
/* C 版 */
int factorial(int n)
{
return n<=1 ? 1 : n*factorial(n-1);
}
# perl 版
sub factorial {
return $_[0] <=1 ? 1 : $_[0] * factorial($_[0]-1);
}
; lisp 版
(defun factorial (n)
(if (<= n 1)
1
(* n (factorial (1- n)))
)
)
Q: 請 trace (逐步追蹤) factorial(3), 請問 n 的值如何變化?
結論: n 不是 一個變數, 而是好幾個變數共用的一個名字。 在談論遞迴以前, 大家就已經知道: 每個副程式 有自己的空間來存放它自己的 局部變數, 所以在不同的副程式當中, 即使出現相同名字的變數也沒有關係: 這些變數彼此之間是獨立的, 只是名字恰好相同而已。 然而若希望電腦能夠處理遞迴的副程式, 這樣還不夠。 必須做到 一個副程式, 它每個正在執行的分身 都要有自己的空間來存放它自己的變數。
我們來 trace 追蹤 以下程式的執行過程:
void main() {
printf(" 1");
A();
printf(" 2");
C();
printf(" 3");
}
void A() {
printf(" 4");
B();
printf(" 5");
C();
printf(" 6");
}
void B() {
printf(" 7");
}
void C() {
printf(" 8");
}
一個副程式開始執行的時候, 系統會分配一塊空間給它, 叫做它的
activation record。 這裡面存放著它的形式參數, 區域變數,
結束時的返回位址 (return address) 等等。 副程式執行結束時, 便從
activation record 當中取得返回位址, 回到 (當初呼叫它的)
上一層副程式繼續執行下一句; 而系統也在此時收回它的 A.R。
同屬於一支執行中程式的所有副程式, 它們的 A.R。 一起放在同一個 stack
上, 先進後出。 有些書把這個 stack 叫做 system stack
(系統堆疊)。 以上面的例子來說, 它執行時 system stack
的變化就如右圖。 印出來的結果為 " 1 4 7 5 8 6 2 8 3"。
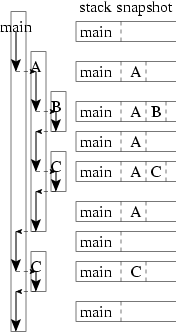
對於不使用遞迴的程式而言, 上述的安排有點多此一舉 (每個副程式分配一塊固定的空間存放 A.R。 中的資料就好了, 何必什麼先進後出?) ; 但是對於使用遞迴的程式而言, 有這麼一個先進後出的 stack 就很重要了 -- 因為一個自己呼叫自己的副程式, 在同一時刻, 可能有好幾個分身都執行到一半, 用動態變化的 stack 才能夠同時存放同一個副程式的好幾個分身的 A.R。 附帶說明, 這些分身並非同時執行, 而是執行到一半冷凍起來, 等著下一層 (比較晚開始執行, 將比較早結束) 的那個分身結束。
作業: 試摹仿右圖, 畫出 factorial(3) 執行的過程當中, stack 的變化。
遞迴思考法之一: 拆成幾個小一號, 長相相同的子問題
回到愚公移山問題, 如何用用遞迴解題呢?
- 問自己一句話, 列舉出這句話的所有可能答案, 不可以有遺漏 (有些許重複沒關係)。
- 每一個可能答案, 是否又變成另外一個 與原問題類似, 但小一號 的問題?
- 把這些小一號 (但其實還是很困難) 的問題, 以不負責任的態度發包給別人去解決。
- (我還是搞不清楚這些小一號的問題是如何解決的; 不過那不重要, 有答案就好)
- 整理這些小一號問題的答案, 從這裡拼湊出原來問題的答案。
- 最小號, 不能夠再拆開的問題, 必須自己動手解決, 不可以無限制地發包下去。
先以 subset sum 問題為例。 首先自問一個很簡單的問題: 答案裡面究竟有沒有包含 x(1)? 只有兩種可能:
- 沒有 -- 那麼原問題可以化簡為 "從 n-1 個整數中挑出數個使和為 s"。 還是很困難嗎? 不必擔心, 有人會幫我解。
- 有 -- 那麼原問題可以化簡為 "從 n-1 個整數中挑出數個使和為 s-x(1)"。 還是很困難嗎? 不必擔心, 有人會幫我解。
把這兩種情況都試過一遍, 我們的責任就完成了。 當然, 如果只有 0 個整數可以挑, 那麼答案很簡單: s 若是 0, 答案就是空集合; s 若是 0, 答案就是不可能, 這種情況自然就不必再遞迴。
順便一提, 老鼠會其實也不過就是一種遞迴, 只是這個遞迴有 bug -- 它的終止條件沒有明確地講出來, 所以有許多相信的人就不會想到自己可能是 「只付出不回收」 的最下層。 一旦入會, 為了避免自己成為最下層, 就自動自發地努力遞迴幫老鼠頭解決問題 (賺更多的錢)。 但事實上從數量上來說, 最下層註定佔老鼠會人口結構的絕大多數。 又順便再提, 散佈封閉檔案格式諸如 .doc 檔 也有類似效果, 不同的是受益者只有一家公司; 參與者非但沒有受益反而受害, 更妙的是可憐的參與者一邊罵啟動遞迴的受益者壟斷市場, 一邊還是繼續用力地幫忙遞迴 ... :-)
遞迴思考法之二: 保守悲觀地估計需要列舉多少情況
有一些比較簡單的遞迴程式, 可以參考下圖, 以 「粗略保守估計工作量」
的方式寫出。 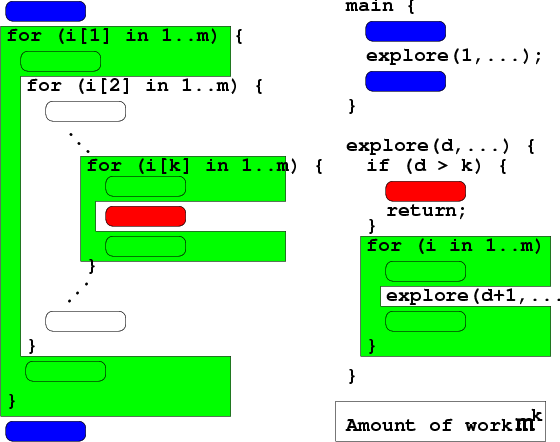
先粗略保守估計 (可高估, 不可低估) 會產生多少種可能狀況? 如果將答案編碼, 通常只是一個很簡單的 排列組合或遞迴關係式 問題。 以騎士問題為例, 總共有多少條不同的路徑要試呢? 先問自己, 你要如何印出答案? 每條路徑可以用 0-1-3-7-6-3-0-2-7-... 的方式表示 (每步可有 0 到 7 共 8 種可能的方向), 所以需要逐一檢查的不同路徑, 最多不會超過 8^24 條。
從上面得到的數學式, 就可以看出 「愚公移山法」 的程式要怎麼寫: 估計出來的大約工作量若是 m^k, 則程式的長相將是 k 個層層相疊的迴圈, 每個迴圈重複 m 次。 以騎士問題為例, 應有 24 個層層相疊的迴圈, 每個迴圈執行 8 次。
如果 k 是比較大的數字, 甚或是變數, 那麼這個問題可能就適合用遞迴來解決。 k 很大表示你的程式需要縮排很多層, 光是讀起來就很礙眼。 而且每層迴圈的長相其實都很類似, 一個好的程式設計師不會放任自己 「勤於動手複製卻懶得動腦簡化」。 (提示: 類似而重複出現的程式碼, 就是值得改進刪減的地方!) 像左圖中綠色迴圈部分既然重複出現, 不如只寫一次, 然後在迴圈當中放一句 「自己呼叫自己」。 效果就像在電梯裡面放兩面相對的鏡子一樣, 鏡中有鏡, 鏡中又有鏡...
一般的遞迴副程式都會有一個記錄「深入層次」參數, (叫它 d 好了) 每進一層就加 1, 它的值代表我們正要進入這 k 層相疊迴圈的第幾層。 (或者說它代表這是孫悟空第幾代的頭髮)
在遞迴的副程式內, 第一句話應該是馬上檢查是否已進入最內層迴圈, 可以終止遞迴了。 這時你所面對的已是最小號的問題, (圖的紅色部分) 不僅不需要再發包, 有時甚至都簡單到連迴圈也不需要。 在 exhaustive search 類的程式中, 通常這就是一組可能解, 此時可以直接測試這組解是否滿足題目的條件; 也可能是一個簡單到窮極無聊的題目, 直接就可以給答案。
原問題當中比較具體的變數 (例如棋盤) 通常都是全域變數。 進入遞迴副程式前, 如果修改了全域變數, 通常都必須在離開遞迴副程式後將它的值還原。 (以前我剛開始學遞迴程式時, 最常忘記做這件事。)
如果估計工作量得到一個遞迴關係式, 亦可直接從遞迴關係式讀出程式的概略長相。 例如 動態規劃 當中的 Matrix Chain Problem ... (待詳述)
除錯時, 應把每個時刻的 A.R。 內容 (各個時刻的 snapshots) 以及當時所有全域變數的值畫出來。
也許你的問題可以用更快的演算法解?
並不是所有看似遞迴可解的問題, 都真的需要遞迴; 不過通常遞迴版總是此類窮舉問題的第一步思考。 一旦寫出遞迴程式之後, 還可以再自問: 遞迴過程當中, 有沒有重複解決的小問題? 若然, 則可能可以改用動態規劃 的方法。 像上述的 matrix chain problem 就屬此類。 把遞迴程式改成動態規劃, 所做的功德奇大無比。 前者經常是 exponential time; 而後者是 polynomial time。 詳見 演算法 講義。
Linear Recursion: 為賦新辭強說愁
你的問題真的需要用遞迴來解嗎? 如果你的遞迴程式的主迴圈當中, 最多只有一個分枝會產生遞迴呼叫, 那麼這其實是一個 linear recursive function, 其實根本就不需要遞迴。 例如二分搜尋法, 二元樹的搜尋, 或上面的階乘都是, 其實只需要一個迴圈垂直地做 n 次 (to do: 畫圖) 就可以了。 這種情況用遞迴, 似乎有點小題大作, 為賦新辭強說愁, 開太空梭上市場買菜。 只是因為它用不用遞迴都可以解, 而且比較簡單, 所以教科書常拿它來做例子。
何時真的需要使用遞迴? 如果你寫出來的是一個 tree recursive function, 也就是說主迴圈內的遞迴呼叫, 有可能發生兩次或兩次以上, 大概就是適合使用遞迴的時機了。
當然上面談的是針對一般的 procedural languages。 至於在 lisp 等 functional programming languages 當中, 因為要避免使用「修改變數內容」的觀念, 所以幾乎所有的函數都用遞迴表示。 在這些環境底下, 文化如此, linear recursion 不算是誤用遞迴。
作業
- 修改 knight.c, 要求騎士最後一格走完後, 下一步正好可以走回原點。 (變成一個 Hamiltonian Circuit 問題)
- 寫一個老鼠走迷宮的程式。
- n 個石子排成一列, 電腦與人輪流自左邊取走, 每次取 1 至 3 顆, 取到最後一顆的贏。
- 將上述每一個程式以純迴圈 (iterative), 非遞迴 (non-recursive) 的方式寫出。 (這篇講義還沒有教怎麼做...)
其他參考資料
- 本頁最新版網址: https://frdm.cyut.edu.tw/~ckhung/b/pr/recursion.php; 您所看到的版本: November 20 2017 17:29:58.
- 作者: 朝陽科技大學 資訊管理系 洪朝貴
- 寶貝你我的地球, 請 減少列印, 多用背面, 丟棄時做垃圾分類。
- 本文件以 Creative Commons Attribution-ShareAlike License 或以 Free Document License 方式公開授權大眾自由複製/修改/散佈。
![[rss feed 圖案]](/~ckhung/i/rss.png)