例: TrendLines 時尚女裝

(本題摘自 Ronald L. Rardin. Optimization in Operations Research. Prentice Hall)

TrendLines 公司生產時尚女裝。 每項產品的單價, 人工及機器成本, 和所使用的布料列表如下:

Fall professional fashions
品名 單價 (元) 人機成本 (元) 所需布料
Wool slacks 300 160 3 yards of wool
2 yards of acetate
Cashmere sweater 450 150 1.5 yards of cashmere
Silk blouse 180 100 1.5 yards of silk
Silk camisole 120 60 0.5 yard of silk
Tailored skirt 270 120 2 yards of rayon
1.5 yards of acetate
Wool blazer 320 140 2.5 yards of wool
1.5 yards of acetate
Fall casual fashions
Velvet pants 350 175 3 yards of velvet
2 yards of acetate
Velvet shirt 200 160 1.5 yards of velvet
Cotton sweater 130 60 1.5 yards of cotton
Cotton miniskirt 75 40 0.5 yard of cotton
Button-down blouse 120 90 1.5 yards of rayon

本季已訂得的布料量及價格如下表:

布料 Wool Acetate Cashmere Silk Rayon Velvet Cotton
量 (yards) 45000 28000 9000 18000 30000 20000 30000
每碼價格 (dollars) 9.00 1.50 60.00 13.00 2.25 12.00 2.50

沒用完未拆封的布料可以退回; 但剪裁剩下的碎布料當然不行。 製作 silk blouse 跟 cotton sweater 都會產生大塊的剩下布料: 2 碼的 silk 裡面, 製作 silk blouse 只會用到 1.5 碼; 為了不浪費剩下的 0.5 碼, 乾脆就直接拿來做 silk camisole。 所以伴隨著每一件生產的 silk blouse, 都會同時生產一件 silk camisole。 (但反之並不必然) 同理, 伴隨著每一件生產的 cotton sweater, 都會同時生產一件 cotton miniskirt。

因為 velvet 材質的時裝很容易退流行, 所以 TrendLines 不希望生產超過 5500 件 velvet pants 也不希望生產超過 6000 件 velvet shirts。 Cashmere sweater 太貴了, 希望不要生產多於 4000 件, 以免賣不出去。 又因為 silk 不好保養, 也因此不好賣, Trendlines 決定 silk blouse 最多只生產 12000 件; silk camisole 最多 15000 件。

市場整體對 wool slack 的需求約有 7000 件, wool blazer 5000 件, 為留住忠誠客戶, TrendLines 希望至少要能滿足 60% 的市場需求。

TrendLines 希望在上述條件下獲得最高利潤。 寫出模型如此檔: trendlines.lp 再以 lp_solve -S4 trendlines.lp 解題, 得到輸出 trendlines.out

"Objective function limits" 的 "From" 與 "Till" 欄位的意義: 這個變數在 objective function 當中的係數, 即使有些變化, 只要落在 From 到 Till 的範圍之內, 最佳解的各變數值還是不會改變; 而此時 objective function 的值也很容易計算。 例如: 在 objective function 中, 若 ws 的獲利從 110 (元/件) 變成 115 (元/件), 則不必重跑 lp_solve 就知道: 新的最佳解, 所有變數值不變, 而總獲利變成 6862930 + (115 - 110) * 4200 = 6883930。 又例如: 在 objective function 中, 若 me 的獲利從 210 (元/件) 變成 200 (元/件), 則不必重跑 lp_solve 就知道: 新的最佳解, 所有變數值不變, 而總獲利變成 6822930

"Dual Values" 最左邊的數字欄位所顯示的是 shadow prices, 單位是: 目標函數/此限制條件。 例如 acetate 那一列, 最左邊的 71.83 單位是 dollars/yard, 表示這個限制條件的右側數值每加 1 (每多一碼的 acetate 布料可用), 總獲利的最佳解將增加 71.83 元。 所以若 acetate 有 30000 碼可用, 則總獲利的最佳解將變成 6862930 + 71.83 * (30000 - 28000) = 7006590。 又例如 rayon 布料若變成 24000 碼, 則總獲利的最佳解將變成 6862930 + 17.75 * (24000 - 30000) = 6756430。

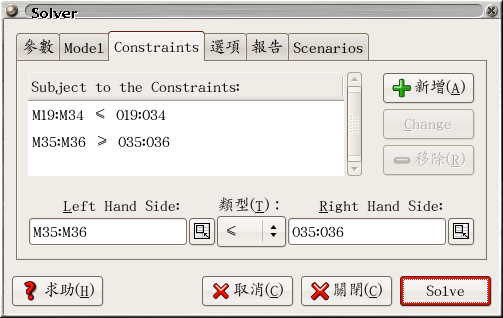
同性質的條件可以一口氣指定 用 gnumeric 建立試算表如此檔: trendlines.gnumeric 注意我們把所有相同方向的限製條件放在一起 (16 個小於等於放一起; 2 個大於等於放一起) 這樣要用 solver 設定限制條件時比較方便, 如圖, "Left Hand Side" 與 "Right Hand Side" 可以選取一整塊連續的區域。 在 solver 的 「報告」 分頁, 選取 「答案」 與 「Sensitivity」。 按下 Solve 之後, 試算表會多出兩個分頁, 裡面的資訊與 lp_solve 所給的相仿。