圖解 Normal Equation 求最小方差 (直覺解釋)

圖解 normal equation 求最小方差 (直覺解釋) Normal Equation: 當矩陣 A 的寬度小於它的高度時, A x = b 的解可用: 滿足 A' (A x - b) = 0 的 x 來近似。

A x 的幾何意義: 當 x 自由變動, A x 產生 A 的 column space。

A x = b 想要有解, b 必須落在 A x 的 column space 當中。

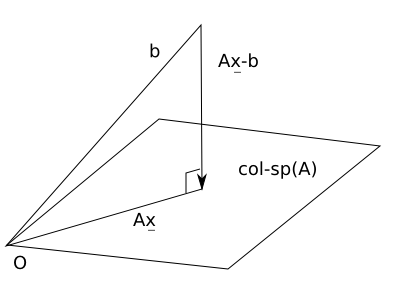
b 若不落在 A x 的 column space 當中, 只好退而求其次: 至少 b 的 投影 projection 必然落在此空間當中 (by definition)。

試圖尋找 x 使得 A x - b 的長度 (也就是誤差值) 最小。

上述誤差的最小值正好發生在誤差向量與 A 的 column space 垂直時, 也就是說, 希望誤差向量落在 A' 的 null space

右圖中的 A 是一個 3x2 的矩陣; 圖中的四邊形標示出 A 的 column space 那個平面; 而 b 則是那個平面之外的一點。 x 是 Ax = b 的最佳近似解。