表達人事物之間的關係 (為什麼要學 Binary Relation 與 Graph)
動機
問題: 如何描述一群人之間, 彼此是否存在某種關係? 為下文解說方便, 每個例子都取了一個名字。
- 「握手」: a 與 b 是否握過手?
- 「愛戀」: a 是否愛戀 b?
- 「通訊錄」: a 的通訊錄當中, 是否有 b 的電話號碼?
- 「溝通」: a 會講的語言當中, 有 b 聽得懂的語言嗎?
- 「和睦」: 舉辦一場宴會, 可否同時邀請 a 與 b 出席? (也許兩人之間有過節)
- 「生下」: a 是 b 的親生父/母嗎?
- 「尊親」: a 是 b 的直系尊血親嗎?
我們也可能對事物與事物之間的關係感到興趣, 例如:
- 「先修」: 一定要修過 a 這門課, 才可以修 b 這門課嗎?
- 「開檔」: a 文書處理軟體所存的檔案, b 文書處理軟體可以開啟嗎?
- 「接壤」: a 國與 b 國的領土是否在陸地上相鄰?
- 「競食」: a 物種的食物與 b 物種的食物是否有交集? (因而可能會競爭/排擠)
- 「整除」: a 可以整除 b 嗎?
- 「小於」: a 小於 b 嗎?
數學家喜歡集合, 所以他可能會這樣表達: 列舉所有答案為 "是" 的排列, 寫成一個集合。 以 「通訊錄」 為例, 如果 a 的通訊錄當中, 有 b 的電話號碼, 就在集合當中列出 (a,b)。 ... (真的舉一個例子) 要表達兩元素 a 與 b 之間有 R 的關係, 有時寫 (a,b) 屬於 R, 有時寫 aRb, 例如用 K 表示 「...的通訊錄當中有...的電話」 此一關係, 則這句話: "a 的通訊錄當中有 b 的電話" 可以簡寫成 "(a,b) 屬於 K" 或 "aKb"
我們一般人可能喜歡用畫圖的方式表達。 還是以 「通訊錄」 為例, 用一個個的圈圈代表每個人, 如果 a 的通訊錄當中, 有 b 的電話號碼, 就從 a 畫一條線指向 b。 ... (真的舉一個例子)
用術語來說, 第一種表示法叫做一個 binary relation 二元關係; 第二種表示法叫做一個 graph 圖, 每個圈圈叫做一個 vertex, 每一條連線叫做一條 edge。 就最基本簡單的應用而言, binary relation 與 graph 兩者要表達的其實都是同一個觀念, 而且是很直覺, 很簡單, 沒學過術語的人也理解的觀念。 下面還有很多二元關係與圖的術語, 一樣都只是某些日常生活直覺觀念的代名詞。 真正有可能造成學習困難的東西是觀念, 而不是術語; 但這篇沒有困難的觀念, 只有一大堆術語, 所以請不要害怕, 只需要牢記。
incident 描述 vertex 與 edge 之間的關係: 如果 vertex X 為 edge y 的 origin (起點) 或 destination (終點), 則稱 X 為 y 的 incident vertex, 也稱 y 為 X 的 incident edge。 adjacent 描述 vertex 與 vertex 之間的關係: 如果兩個 vertices X 與 Y 之間有一條 edge, 則稱 X 與 Y 互為 adjacent vertices。
上述兩種表達方式都是給人看的 (雖然集合表示法有點難讀, ... 不過數學家也是人呵) ; 真正要存入電腦當中時, 用另外兩種表示法比較方便。 adjacency matrix (相鄰矩陣) 用一個二維陣列儲存資訊。 再以 「通訊錄」 為例, 把所有人名列出放在表格的最左邊, 再將所有人名列一次放在表格的最上面。 如果 A 的通訊錄當中, 有 B 的電話號碼, 就在 A 那一列, B 那一行打鉤。 注意: 習慣上讀此類表格都是 左進上出! 這樣的儲存方式, 比較適合儲存 edge 數目眾多的圖 (稱為 dense graph); 對於 edge 數目稀少的圖 (稱為 sparse graph) 而言, 改用 adjacency list (相鄰串列) 比較不浪費空間: 用一個一維陣列, 每個元素後面拖著一個 list。 把所有人名列出放在表格的最左邊, 在每個人後面列出他通訊錄的名單
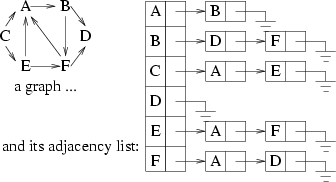
圖 (1) 為一個 graph 及它的 adjacency list; 至於它的 adjacency matrix 如下:
| A | B | C | D | E | F | |
| A | v | |||||
| B | v | v | ||||
| C | v | v | ||||
| D | ||||||
| E | v | v | ||||
| F | v | v |
對稱/不對稱; 相反/互補
有些 binary relation 或 graph 具有對稱的特性: 若 aRb 則 bRa; 以圖來講, 有 edge 的地方, 必然都是雙向互指。 這樣的關係稱為一個 symmetric relation 這樣的圖稱為一個 undirected graph 無向圖。 既然箭頭必然是雙向的, 可以乾脆省略, 只畫連線。 例如 「握手」 與 「接壤」 都是。 還有那些是 symmetric relations / undirected graphs?
至於一般的 binary relation 或 graph, aRb 與 bRa 不見得同時成立, 因此稱為 non-symmetric relation, 或 directed graph 有向圖, 簡稱 digraph。 「溝通」 與 「先修」 例都是。 還有那些是 directed graphs?
有些 binary relation 具有以下特性: 若 aRb 則必然不會 bRa。 這樣的關係稱為一個 asymmetric relation; 以 graph 來說, 就是圖裡面不存在雙向箭頭, 也不存在首尾落在同一 vertex 的 edge。 例如 「生下」 與 「先修」 都是。
有些 binary relation 具有以下特性: 若 aRb 且 bRa 則 a=b。 這樣的關係稱為一個 antisymmetric relation; 以 graph 來說, 就是圖裡面不存在雙向箭頭 (但可以有首尾落在同一 vertex 的 edge)。 例如 「整除」 就是。
把每一對 a 與 b 對調, 所得到的關係叫做原關係的 inverse relation; 這相當於把圖所有的箭頭顛倒過來, 也相當於把 adjacency matrix 沿對角線翻轉, 所以稱為原圖的 transpose。 例如 "a 是 b 的親生父/母嗎?" 的 inverse relation 或 transpose graph 就是: "a 是 b 的親生子/女嗎?"
把一個 relation 裡面, 所有的 "是" 與 "否" 對調, 所得到的 relation, 叫做原關係的 complement relation。 類似地, 把一個 graph 裡面, 所有原本既有的 edges 刪除, 原本不存在的 edges 全部新增 (但不包含 loops), 所得到的 graph, 叫做原圖的 complement graph。 「和睦」 的 complement 就是 「需要避開」。
注意: inverse/transpose 與 complement 不一樣。 "a 可以整除 b 嗎?" 的 inverse/transpose 是: "a 可以被 b 整除嗎?" ; 而它的 complement 則是: "a 除 b 會剩下零頭嗎?"。 "a 愛戀 b 嗎?" 的 inverse/transpose 是: "a 被 b 愛戀嗎?" ; 而它的 complement 則是: "a 對 b 的感覺在朋友範圍之內嗎?" 。 怎麼樣, 看出數學符號的好處了吧? 畫圖或矩陣, 比用文字描述更簡單明瞭多了。
- 本頁最新版網址: https://frdm.cyut.edu.tw/~ckhung/b/dm/brgr.php; 您所看到的版本: November 20 2016 21:23:48.
- 作者: 朝陽科技大學 資訊管理系 洪朝貴
- 寶貝你我的地球, 請 減少列印, 多用背面, 丟棄時做垃圾分類。
- 本文件以 Creative Commons Attribution-ShareAlike License 或以 Free Document License 方式公開授權大眾自由複製/修改/散佈。
![[rss feed 圖案]](/~ckhung/i/rss.png)